控制图的原理
日期：2018-09-05 / 人气： / 来源：www.biglss.com / 热门标签： 控制图的原理
欢迎您访问博革咨询官网！博革咨询是中国首家整合精益生产/六西格玛/流程再造的咨询公司，专注于提供 精益生产、6S现场管理、TPM设备管理、精益工厂布局、专业目视化、精益供应链、精益研发、六西格玛管理、智能制造等综合性问题解决方案并负责落地实施。
全国咨询热线：021-62373515、157-2153-3189
我们承诺：见效快、易复制，目标必对赌！
一.控制图的原理－波动分布
控制图观点认为：
（1）当过程仅受随机因素影响时，过程处于统计控制状态（简称受控状态）；由于过程波动具有统计规律性，当过程受控时，过程特性一般服从稳定的随机分布；
（2）当过程中存在系统因素的影响时，过程处于统计失控状态（简称失控状态）。而失控时，过程分布将发生改变。
SPC正是利用过程波动的统计规律性对过程进行分析控制的。因而，它强调过程在受控和有能力的状态下运行，从而使产品和服务稳定地满足顾客的要求。
二.控制图的原理－统计
受控状态是生产过程追求的目标，此时，对产品的质量是有把握的。控制图即是用来监测生产过程状态的一种有效工具。
控制图的统计学原理，令W为度量某个质量特性的统计样本。假定W的均值为μ，而W的标准差为σ。于是，中心线、上控制限和下控制限分别为
UCL =μ +Kσ
CL =μ
LCL =μ －Kσ
式中，K为中心线与控制界限之间的标准差倍数 ， Kσ表示间隔宽度。
正常情况下点子分布是正态的，落在控制界限之内的概率远大于落在控制界限之外的概率。反之，若点子落在控制界限之外，可能是属于正常情况下的小概率事件发生，也可能是过程异常发生，相对来讲，后者发生的概率要大得多。因此，我们宁可以为后者情况发生，这正是控制图的统计学原理。
点子落在控制界限之内是否一定处于稳态？点子落在控制界线之外是否一定出现异常？这两个问题的回答都是否定的。
更为科学的判断应根据概率统计方法对过程进行定量分析，精确计处出状态的概率值之后再进行过程状态判断。
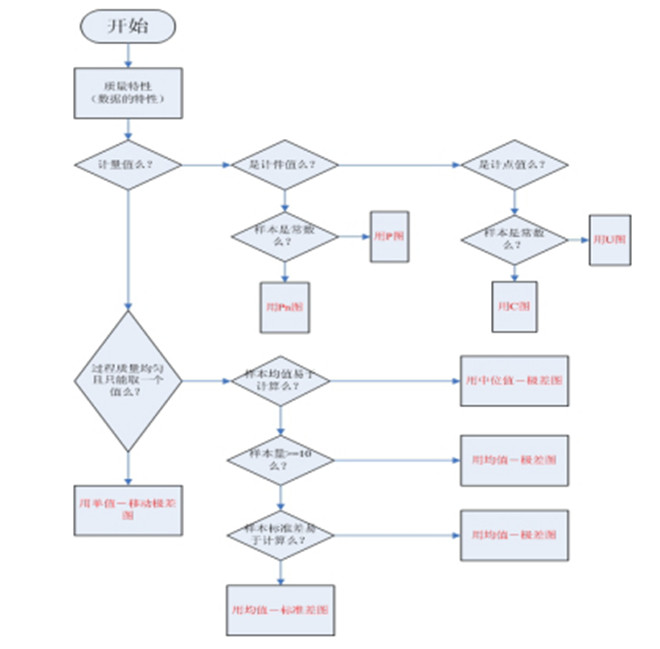
三.控制图的原理－分类1
各控制图用途：
均值－极差控制图: 是最常用、最基本的控制图，它用于控制对象为长度、重量、强度、纯度、时间和生产量等计量值的场合。
均值－标准差控制图: 次图与上图类似，极差计算简便，故R图得到广泛应用，但当样本大小或0>10或12时，应用极差估计总体标准差的效率减低，最好应用S图代替R图。
中位数－极差控制图: 由于中位数的计算比均值简单，所以多用于现场需要把测定数据直接记入控制图进行管理的场合。
均值－移动极差控制图: 多用于下列场合, (1)采用自动化检查和测量对每一个产品都进行检验的场合； (2)取样费时、昂贵的场合； (3)如化工等过程，样品均匀，多抽样也无太大意义的场合。由于它不像前三种控制图那样能取得较多的信息，所以它判断过程变化的灵敏度也要差一些。
P控制图：用于控制对象为不合格品率等计数值质量指标的场合。这里需要注意的是，在根据多种检查项目总起来确定不合格品率的场合，当控制图显示异常后难于找出异常的原因。因此，使用P图时应选择重要的检查项目作为判断不合格品的依据。
（1）连续25个点都在控制限内（显著性水平为：0.0654）。
（2）连续35个点至多一个点落在控制限外（显著性水平为：0.0041） 。
（3）连续100个点至多两个点落在控制限外（显著性水平为：0.0026） 。
Pn控制图：用于控制对象为不合格品数的场合。设n为样本大小，P为不合格品率，则Pn为不合格品个数。由于计算不合格品率需要进行除法，比较麻烦。所以在样本大小相同的情况下，用此图比较方便。
C控制图：用于控制一部机器、一个部件、一定的长度、一定的面积或任何一定的单位中所出现的缺陷数目。例如，铸件上的砂眼数，机器设备的故障数等等。
U控制图：当样品的大小变化时应换算成每单位的缺陷数并用U控制图。
通用控制图：
四.控制图的原理－判稳准则
（1）连续25个点都在控制限内（显著性水平为：0.0654）。
（2）连续35个点至多一个点落在控制限外（显著性水平为：0.0041） 。
（3）连续100个点至多两个点落在控制限外（显著性水平为：0.0026） 。
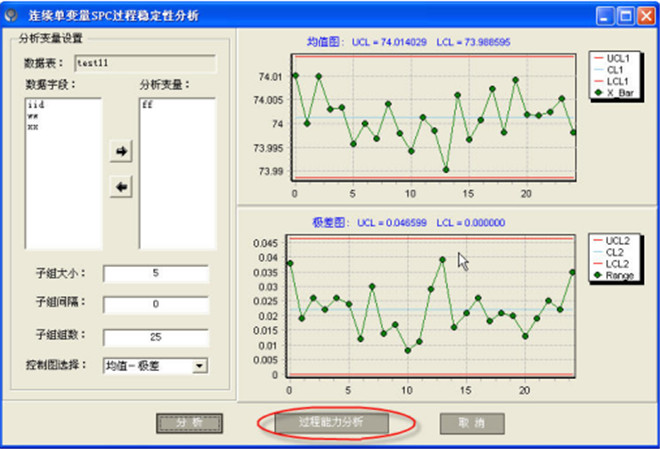
五.控制图的原理－计量型稳定
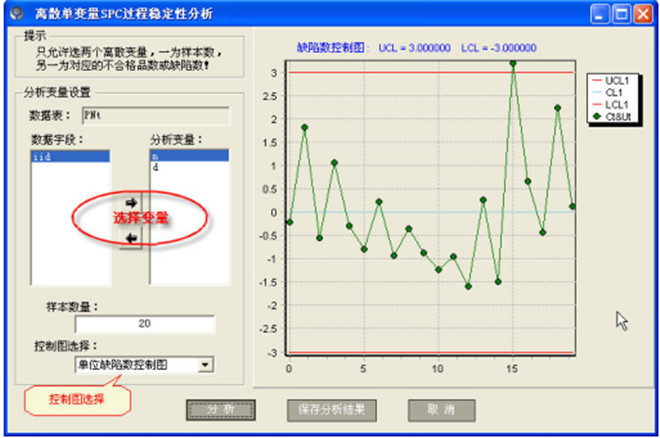
六.控制图的原理－计数型不稳定
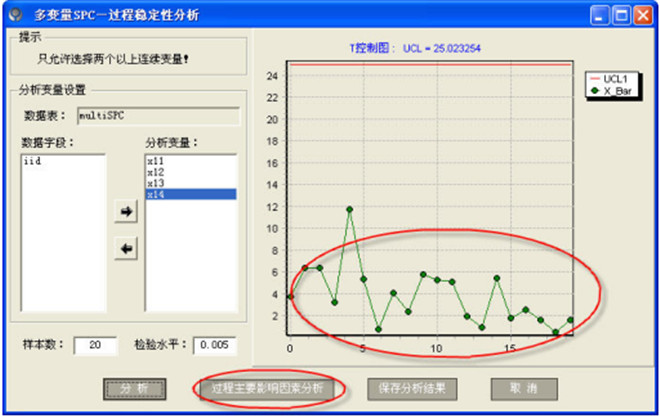
七.控制图的原理－多变量型
八.控制图的原理－分类2
分析用控制图（判稳）。
控制用控制图（判异）。
联系：分析用控制图通过判稳准则分析过程的稳定性，并得出过程的控制限应用到控制用控制图，通过判异准则判断/预测过程的稳定性。
九.控制图的原理－判异准则
1.点在控制界限外或界限上。
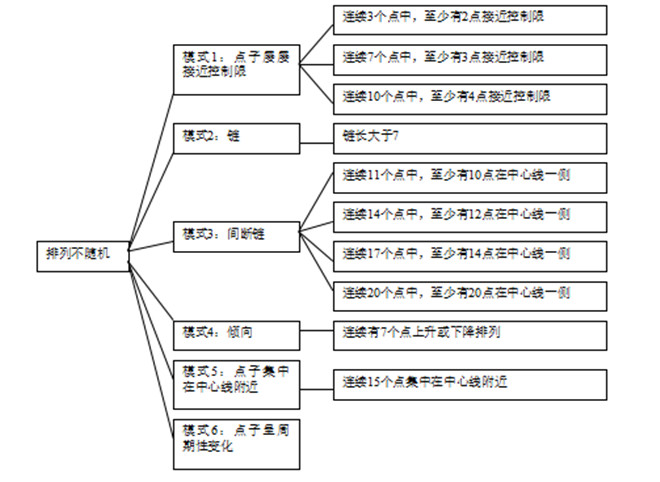
2.排列不随机：
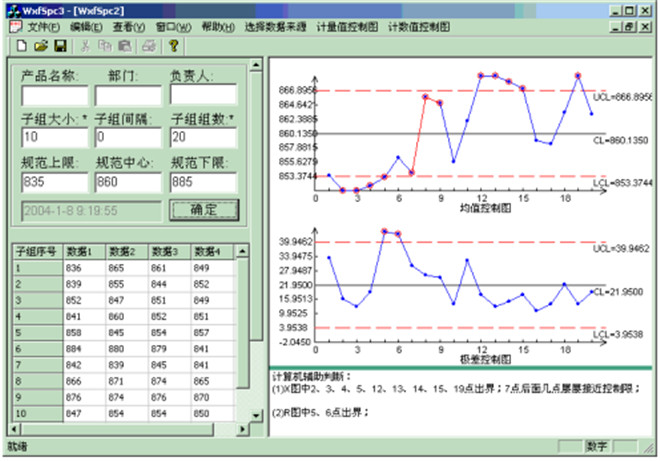
十.控制图的原理－判异准则程序实现示例
作者：博革精益六西格玛
咨询采购表
精益生产怎么做？六西格玛咨询怎么做？项目周期是多少？大概需要多少费用？
我是什么企业？目前需要解决的问题是什么？预算周期是多少？想要达到什么效果？
欢迎您浏览博革咨询官方网站！我们专注于精益生产咨询、六西格玛咨询、精益供应链咨询、5S6S现场管理、TPM设备管理咨询、工厂布局规划、目视化看板设计等领域的落地咨询；若对本页面内容不感兴趣或想了解更多与您企业、行业相关的资讯，可通过以下方式寻找解决方法：
（1）工作时间可拨打我们的全国咨询热线：15721533189，021-62373515 进行咨询；
（2）在网站栏目右侧“搜索框” 输入您感兴趣的关键词，搜索相关内容；
（3）点击左侧“在线咨询”按钮， 您可以和我们的专家老师在线咨询；
（4）非工作时间请点击网站下方的“留言” 按钮，留下您的联系方式和需要咨询的内容，我们将安排专业顾问给您解答；
（5）
入群方式：扫描左图二维码，添加小博微信好友，通过认证后，加入精益生产VIP会员微信群。
热销课程 Hot
相关内容 Related
- 2021年中质协六西格玛考试时间及报名通知07-05
- 十九点6西格玛管理学习术语总结03-30
- 2020年六西格玛黑带考试试题及证书经验分享03-19
- 六西格玛水平的缺陷率03-16
- 六西格玛（6 Sigma）设计-DFSS的步骤03-08
- 六西格玛管理的新发展-精益六西格玛03-05